【OI笔记】网络流

前言

重操旧业！

正文

最大流

教程去OI-Wiki上看吧，我懒得打字了。   看了数不胜数的博客，发现没有一个用vector实现的，我大vector就这么没有面子？   其实大家不用vector的最主要原因应该是vector做不到O(1)查找反向边。但是。。。真的不行吗？   在经过一个晚自习的《充分》debug下，我成功地利用神奇的**pair<>**做到了O(1)查找反向边，就是关键代码有亿点点难看

1
2
3
//没错，C++可以pair套pair!
//三个数值分别代表to,flow以及反向边的vector下标。
vector <pair<pair<ll,ll>,ll > > edge[MAXN];
1
2
3
4
5
6
7
8
9
10
//这是加入代码
void add(int tmp1,int tmp2,int tmp3)
{
    edge[tmp1].push_back(make_pair(make_pair(tmp2,tmp3),0));
    edge[tmp2].push_back(make_pair(make_pair(tmp1,0),0));
    ll pos1=edge[tmp1].size()-1;
    ll pos2=edge[tmp2].size()-1;
    edge[tmp1][pos1].second=pos2;
    edge[tmp2][pos2].second=pos1;
}

&emsp下面就放上vector版的网络最大流代码吧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
//Luogu P3376
#include <bits/stdc++.h>
#define MAXN 200005
using namespace std;
typedef long long ll;
vector <pair<pair<ll,ll>,ll > > edge[MAXN];
ll n,m,s,t;
ll ans;
ll dep[MAXN];
ll ct;
void add(int tmp1,int tmp2,int tmp3)
{
    edge[tmp1].push_back(make_pair(make_pair(tmp2,tmp3),0));
    edge[tmp2].push_back(make_pair(make_pair(tmp1,0),0));
    ll pos1=edge[tmp1].size()-1;
    ll pos2=edge[tmp2].size()-1;
    edge[tmp1][pos1].second=pos2;
    edge[tmp2][pos2].second=pos1;
}
void init()
{
    // memset(head,-1,sizeof head);
    cin>>n>>m>>s>>t;
    for (ll i=1;i<=m;i++)
    {
        ll tmp1,tmp2,tmp3;
        cin>>tmp1>>tmp2>>tmp3;
        add(tmp1,tmp2,tmp3);
    }
}
bool bfs()
{
    memset(dep,0,sizeof dep);
    queue <ll> q;
    dep[s]=1;
    q.push(s);
    while (!q.empty())
    {
        ll u=q.front();
        q.pop();
        for (ll i=0;i<edge[u].size();i++)
        {
            ll v=edge[u][i].first.first;
            ll di=edge[u][i].first.second;
            if (!dep[v] && di)
            {
                dep[v]=dep[u]+1;
                q.push(v);
                if (v==t) return 1;
            }
        }
    }
    return 0;
}
ll dfs(ll u,ll flow)
{
    // cout<<ans<<endl;
    if (u==t) return flow;
    ll re=0;
    // cout<<u<<" "<<t<<endl;
    for (ll i=0;i<edge[u].size();i++)
    {
        // cout<<i<<endl;
        ll v=edge[u][i].first.first;
        ll& di=edge[u][i].first.second;
        ll& fan=edge[v][edge[u][i].second].first.second;
        if (dep[v]==dep[u]+1 && di)
        {
            ll tmp=dfs(v,min(di,flow));
            if (!tmp) dep[v]=0;
            re+=tmp;flow-=tmp;
            di-=tmp;
            fan+=tmp;
            if (!flow) break;
        }
    }
    return re;
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    freopen("in.in","r",stdin);
    init();
    while (bfs())
    {
        while (ll tmp=dfs(s,1e9))
        {
            ans+=tmp;
        }
    }
    cout<<ans<<endl;
}

Vector YYDS!!!

费用流

先放代码，具体教程就到OI-WIKI或其它博客上学习吧（本人太菜写得不好）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include <bits/stdc++.h>
#define MAXN 10005
using namespace std;
int n,m,s,t;
vector <pair<pair<int,int>,pair<int,int> > > edge[MAXN];
int cost[MAXN],flow[MAXN];
bool vis[MAXN];
int pre[MAXN],last[MAXN];
int maxf,minc;
void add(int tmp1,int tmp2,int tmp3,int tmp4)
{
    edge[tmp1].push_back(make_pair(make_pair(tmp2,tmp3),make_pair(0,tmp4)));
    edge[tmp2].push_back(make_pair(make_pair(tmp1,0),make_pair(0,tmp4*-1)));
    int pos1=edge[tmp1].size()-1;
    int pos2=edge[tmp2].size()-1;
    edge[tmp1][pos1].second.first=pos2;
    edge[tmp2][pos2].second.first=pos1;
}
void init()
{
    cin>>n>>m>>s>>t;
    for (int i=1;i<=m;i++)
    {
        int tmp1,tmp2,tmp3,tmp4;
        cin>>tmp1>>tmp2>>tmp3>>tmp4;
        add(tmp1,tmp2,tmp3,tmp4);
    }
}
bool spfa()//for costt
{//to,flow,fan,costt
    memset(cost,0x3f3f3f,sizeof cost);
    memset(flow,0x3f3f3f,sizeof flow);
    memset(vis,0,sizeof vis);
    pre[t]=-1;
    queue <int> q;
    q.push(s);
    cost[s]=0;
    vis[s]=1;
    while (!q.empty())
    {
        int u=q.front();
        q.pop();
        vis[u]=0;
        for (int i=0;i<edge[u].size();i++)
        {
            int v=edge[u][i].first.first;
            int co=edge[u][i].second.second;
            int fl=edge[u][i].first.second;
            if (fl && cost[v]>cost[u]+co)
            {
                cost[v]=cost[u]+co;
                pre[v]=u;
                last[v]=i;
                flow[v]=min(flow[u],fl);
                if (!vis[v])
                {
                    vis[v]=1;
                    q.push(v);
                }
            }
        }
    }
    return pre[t]!=-1;
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    freopen("in.in","r",stdin);
    init();
    while (spfa())
    {
        // cout<<"adf"<<endl;
        int now=t;
        maxf+=flow[now];
        minc+=flow[now]*cost[now];
        while (now!=s)
        {
            int fa=pre[now];
            int pos=last[now];
            edge[fa][pos].first.second-=flow[t];
            edge[now][edge[fa][pos].second.first].first.second+=flow[t];
            now=fa;
        }
    }
    cout<<maxf<<" "<<minc<<endl;
    return 0;
}

代码不是关键，关键是如何证明，因为在这份代码上面缺少了我们熟悉的bfs与dfs，还缺少了我们熟悉的dep。但我们在代码中还是可以。。。等等，这貌似就是EK+SPFA吧。。。   那就不用证明了，结论就是 EK+SPFA 阿巴阿巴阿巴阿巴

特殊情况处理

1.费用流中的负环

其实不只是负环，应该说每一条费用为负数的边（有补贴～～～）。

以最小费用最大流为例，我们可以通过退流来消除费用为负数的边。 具体过程： 不妨设有一条从u到v的容量为c费用为d的边（d<0）。 先强制满流，把答案加上c×d。 之后，从u到T，S到v各连一条容量为c，费用为0的边，用来调整流量。这两条边要使用手段强制满流。 最后，连一条从v到u的容量为c费用为−d的边，用于退流。 这样就没有负环了。 (节选自：https://www.cnblogs.com/lnzwz/p/12327725.html）

但是，我好像，看懂了，又没完全懂。所以，上图！ 比如说，我们有这样一条负边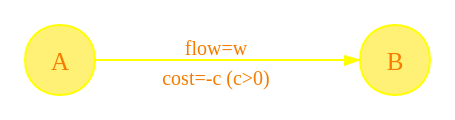： 那么，他就会变成这样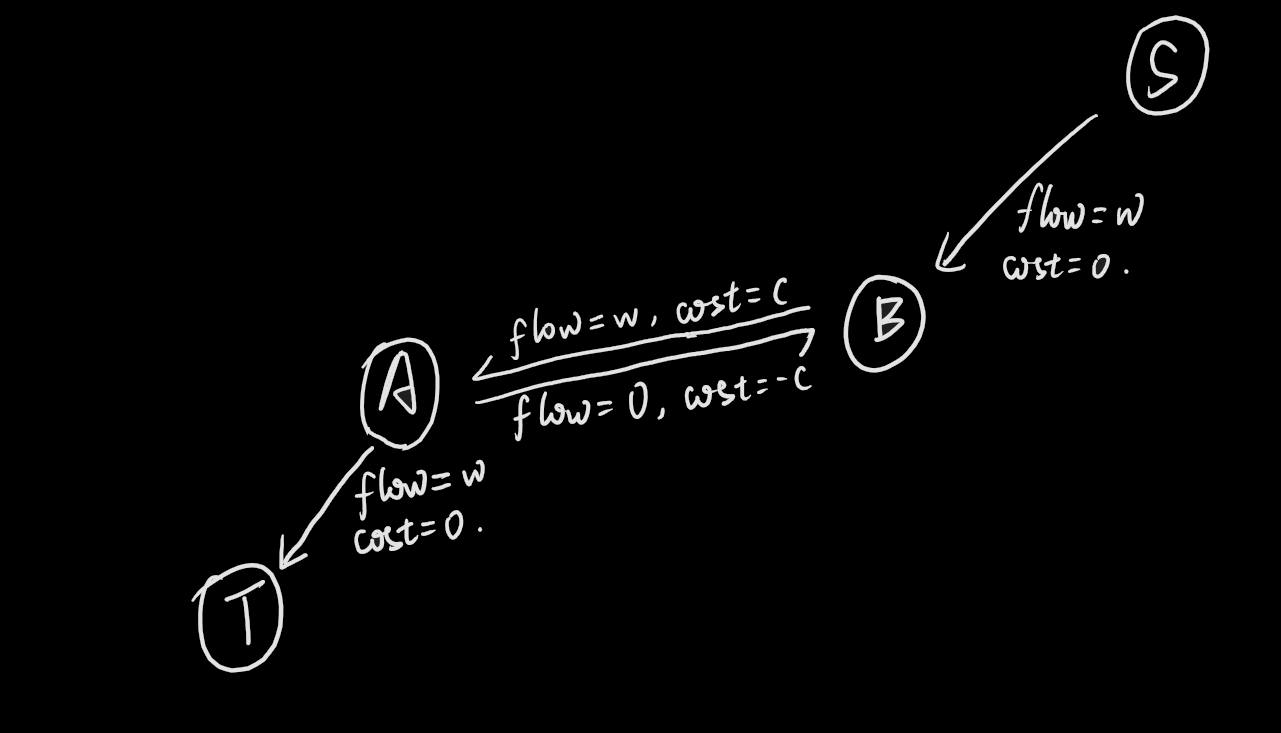： 我为什么，记住就完了

Warning

1.踩坑事故

1) 数组不要开小了

这是老生常谈的问题，可能导致TLE或RE，一般可以通过极限数据来发现问题。

2) 记得开long long

翻车现场 一定一定一定一定记得开long long！

Remember to open long long 開くことを忘れないでくださいlong long Mos harroni të hapni long long ຈືຂໍ້ມູນການເປີດ long long തുറക്കാൻ ഓർമ്മിക്കുക long long ဖွင့်ရန်သတိရပါ long long 記得開long long ចាំបើក long long อย่าลืมเปิด long long Не забудьте открыть long long 여는 것을 기억하십시오 long long

3) 把u,v打反，或u,i打反

E.g:

1
2
//Wrong!
flow[v]=min(flow[v],fl);
1
2
//Correct
flow[v]=min(flow[u],fl);

To Be Continued

oi-note
#OI笔记
【OI笔记】网络流
https://学习.fun/oi-note/network-flow/
Author
Stephen Zeng
Posted on
July 13, 2021
Licensed under