前言
Splay其实并不是一种数据结构,而是给另一种数据结构进行优化的方式。
预备
Splay是建立在二叉查找树(BST)的基础上的,所以要学会Splay,就必须先了解二叉查找树。二叉查找树的形态是一颗形如这样的二叉树: OI-Wiki ,大致操作就是**和当前子树的根节点的val值进行比较,若大于,则往又查找;若小于,则往左查找。**这样的话,我们在进行中序遍历的时候呈现出来的val值就是一个递增的序列,看图:
正文
Why Splay?
在预备中我们讲到了,二叉查找树。但是,为什么要用到他呢?因为她 省时间还不占空间 唯一的槽点就是码量巨TM大 ,这也是为什么在实际比赛中用不到它,在做一般的题目时有种杀鸡用牛刀的感觉。我线段树它不香么。那么,由于使用的是二叉树,时间复杂度就可以降到log级别。燃鹅,真的是这样么?在经历几次插入的折磨后,我们的二叉树可能就会变成这样:
旋转
Warning:接下来的内容可能需要几分钟。
Step 1
Step 2
Step 3
右旋 ,而左旋与之完全镜像,如图:
验证
那么,这样子会不会对原图有修改呢?有,肯定有,你看C节点很明显被提上来一层(dep[c]++)。但是,这样旋转对中序遍历又没有影响,我们举例说明:
C点的爸爸改为A
B点的爸爸改为C
A点的左儿子改为C
B点的左儿子改为2,即C点原来的右儿子
C点的右儿子改为B
我们称这一过程为rotate,代码在下面:
1 2 3 4 5 6 7 8 9 10 11 12 void rotate (int x) int a=t[t[x].fa].fa;int b=t[x].fa;int c=x;0 ]=c;0 ]=t[c].ch[1 ];1 ]=b;return ;
这是右旋,那么左旋我们需要专门写一个函数么?不要,不要,千万不要,如果又写函数,Splay哪有美好的未来?哪有美好的前程?平衡树哪有栋梁之材? 前面我们说过,左旋与右旋是完全相反的,即左旋的步骤是这样的:
C点的爸爸改为A
B点的爸爸改为C
A点的右儿子改为C
B点的右儿子改为2,即C点原来的左儿子
C点的左儿子改为B
所以,我们可以这样写:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 void rotate (int x) int a=t[t[x].fa].fa;int b=t[x].fa;int c=x;int opt;if (t[c].val<t[b].val) opt=0 ;else opt=1 ;1 -opt];1 -opt]=b;return ;
或者高级一点,把if去掉
1 2 3 4 5 6 7 8 9 10 11 12 13 void rotate (int x) int a=t[t[x].fa].fa;int b=t[x].fa;int c=x;int opt=t[c].val>t[b].val;1 -opt];1 -opt]=b;return ;
那么,这就是我们旋转步骤了。 return 0;
Splay
Splay的精髓就在于如何旋转。如图: 所谓类型,即一个节点是其父亲的左/右儿子。
使用
那么,我们什么时候Splay?看代码吧: P3369 【模板】普通平衡树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 #include <bits/stdc++.h> #define MAXN 500005 #define re register using namespace std;int root,tot;struct node {int ch[2 ];int ff;int cnt;int val;int son;void push_up (int x) 0 ]].son+edge[edge[x].ch[1 ]].son+edge[x].cnt;void rotate (int x) int y=edge[x].ff;int z=edge[y].ff;int k=edge[y].ch[1 ]==x;1 ]==y]=x;1 ];1 ]].ff=y;1 ]=y;push_up (y);push_up (x);void splay (int x,int goal) while (edge[x].ff!=goal)int y=edge[x].ff;int z=edge[y].ff;if (z!=goal)0 ]==x)^(edge[z].ch[0 ]==y)?rotate (x):rotate (y);rotate (x);if (!goal) root=x;void ins (int x) int u=root;int ff=0 ;while (u && edge[u].val!=x)if (u) edge[u].cnt++;else if (ff) edge[ff].ch[x>edge[ff].val]=u;0 ]=edge[tot].ch[1 ]=0 ;1 ;splay (u,0 );void find (int x) int u=root;if (!u) return ;while (edge[u].ch[x>edge[u].val] && x!=edge[u].val)splay (u,0 );int nex (int x,int f) find (x);int u=root;if ((edge[u].val>x && f) (edge[u].val<x && !f)) return u;while (edge[u].ch[f^1 ]) 1 ];return u;void del (int x) int la=nex (x,0 );int ne=nex (x,1 );splay (la,0 );splay (ne,la);int de=edge[ne].ch[0 ];if (edge[de].cnt>1 )splay (de,0 );else edge[ne].ch[0 ]=0 ;int kth (int x) int u=root;if (edge[u].son<x)return 0 ;while (true )int y=edge[u].ch[0 ];if (x>edge[y].son+edge[u].cnt)1 ];else if (edge[y].son>=x) u=y;else return edge[u].val;int main () sync_with_stdio (0 );tie (0 );ins (INT_MAX);ins (INT_MAX*-1 );int q;for (int i=1 ;i<=q;i++)int opt,tmp;switch (opt)case 1 :ins (tmp);break ;case 2 :del (tmp);break ;case 3 :find (tmp);cout<<edge[edge[root].ch[0 ]].son<<endl;break ;case 4 :cout<<kth (tmp+1 )<<endl;break ;case 5 :cout<<edge[nex (tmp,0 )].val<<endl;break ;case 6 :cout<<edge[nex (tmp,1 )].val<<endl;break ;return 0 ;
码量巨大。。。
总结
Splay是一个很优秀的算法,它能够很好地对平衡树进行动态调整,能在log级别的时间下完成插入,查询,修改及许多区间操作。但是,相比线段树,Splay,或者说平衡树,的码量太过庞大,且细节很多,不易检查,所以在真正比赛时我们能用线段树绝不用平衡树。 维护平衡树还有其它许多算法,例如不用旋转的Treap,这个算法可以实现平衡树的可持久化,不过我们后面再说吧 是我太菜了。 GB。
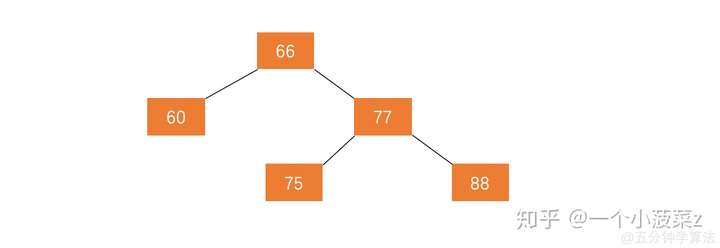 具体查找操作看OI-Wiki,大致操作就是**和当前子树的根节点的val值进行比较,若大于,则往又查找;若小于,则往左查找。**这样的话,我们在进行中序遍历的时候呈现出来的val值就是一个递增的序列,看图:
具体查找操作看OI-Wiki,大致操作就是**和当前子树的根节点的val值进行比较,若大于,则往又查找;若小于,则往左查找。**这样的话,我们在进行中序遍历的时候呈现出来的val值就是一个递增的序列,看图:  至于插入与删除,真是一眼难尽,还是老老实实去wiki上看吧。
至于插入与删除,真是一眼难尽,还是老老实实去wiki上看吧。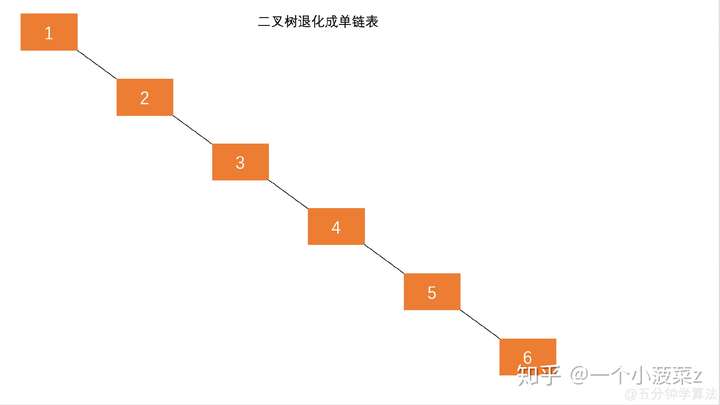 没错,这也是一颗二叉树。但是退化成这样之后,时间又变成O(n)了。。。 SH*TTTTTTTTTTTTTT 这时候,我们可以通过一种方法叫做**“旋转”**来重新使这棵树平衡,而旋转也是二叉树的基本操作。
没错,这也是一颗二叉树。但是退化成这样之后,时间又变成O(n)了。。。 SH*TTTTTTTTTTTTTT 这时候,我们可以通过一种方法叫做**“旋转”**来重新使这棵树平衡,而旋转也是二叉树的基本操作。 旋转分为两种,一种看图:
旋转分为两种,一种看图:  (别问我为什么是图不在中间,鬼知道Microsoft WhiteBoard她是怎么排版的) 什么,你说你搞不懂?那我们一步一步来剖析: 注意,这只是帮助你理解如何旋转,在程序中无需体现也无法体现
(别问我为什么是图不在中间,鬼知道Microsoft WhiteBoard她是怎么排版的) 什么,你说你搞不懂?那我们一步一步来剖析: 注意,这只是帮助你理解如何旋转,在程序中无需体现也无法体现

 return 0; 这种旋转被称之为右旋,而左旋与之完全镜像,如图:
return 0; 这种旋转被称之为右旋,而左旋与之完全镜像,如图:  (好像我挪一挪位置这个图又到中间来了)
(好像我挪一挪位置这个图又到中间来了) 看,没有影响! 我们先翻译成中文,右旋的步骤就是:
看,没有影响! 我们先翻译成中文,右旋的步骤就是: + 如果x的父亲是根节点,直接将 左旋或右旋(图1、2)。 + 如果x的父亲不是根节点,且x和父亲的儿子类型相同,首先将其父亲左旋或右旋,然后将 x右旋或左旋(图3、4)。 + 如果x的父亲不是根节点,且x和父亲的儿子类型不同,将x左旋再右旋、或者右旋再左旋(图5、6)。 所谓类型,即一个节点是其父亲的左/右儿子。
+ 如果x的父亲是根节点,直接将 左旋或右旋(图1、2)。 + 如果x的父亲不是根节点,且x和父亲的儿子类型相同,首先将其父亲左旋或右旋,然后将 x右旋或左旋(图3、4)。 + 如果x的父亲不是根节点,且x和父亲的儿子类型不同,将x左旋再右旋、或者右旋再左旋(图5、6)。 所谓类型,即一个节点是其父亲的左/右儿子。